高中数学对数与对数函数的解题思路与方法
原创|2015-10-12 16:15
【课题】对数与对数函数
【学习目的】解决学生在函数综合性问题解答中的困难，找到更多解题思路与方法。
【重点】1、对数函数的概念;
2、对数函数的图像和性质。
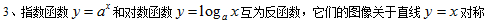
【关键】根据题目的具体情况把问题分解为若干小问题分类解决，再整合。
【定义】对数：一般来说，如果a(a大于0，且a不等于1)的b次幂等于N，那么数b叫做以a为底N的对数，记作log aN=b,读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。
对数函数：一般地，函数y=log(a)X，(其中a是常数，a>0且a不等于1)叫做对数函数，它实际上就是指数函数的反函数，因此指数函数里对于a的规定，同样适用于对数函数。
【详细解析】
对数函数的一般形式为，它实际上就是指数函数的反函数。因此指数函数里对于a的规定，同样适用于对数函数。对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形，因为它们互为反函数。
(1)对数函数的定义域为大于0的实数集合。
(2)对数函数的值域为全部实数集合。
(3)函数总是通过(1，0)这点。
(4)a大于1时，为单调递增函数，并且上凸;a小于1大于0时，函数为单调递减函数，并且下凹。
(5)显然对数函数无界。
【常见考法】高中函数是段考和高考必考的内容，多以三大题型考查学生对对数函数的图像和性质的应用能力。题目难度一般较大，在高考中也经常和导数等知识联合考查。
【误区提醒】
智择优推荐您继续阅读：
